- Инновации
- Статьи о применении синтетических инструментов
- Портфельная Торговля
Оптимизация портфеля с помощью метода PQM (часть 2)
Предположим, что инвестор действительно готов принять более высокий уровень риска для повышения ожидаемой доходности портфеля. Пусть максимально допустимое стандартное отклонение доходности портфеля составляет 2.5%. Проведем процедуру оптимизации весовых коэффициентов для поиска максимальной доходности портфеля при наличии дополнительного ограничения по стандартному отклонению (оно не должно превышать 2.5%).
Решение приводит нас к следующему составу портфеля Р3: вновь самый большой вес (61.63%) получили акции MCD. Затем по убыванию весов расположились DIS (21.74%), HON (14.17%), IBM (1.61%) и HD (0.84%). Акции KO получили нулевой вес и не вошли в состав портфеля Р3.
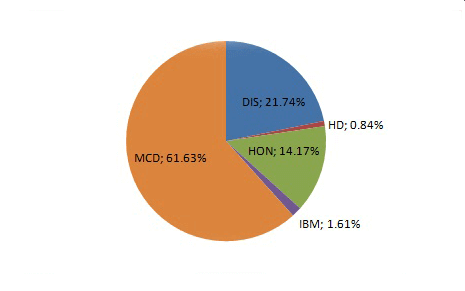
В результате, полученный путем изменения весов для максимизации доходности, портфель (Р3), при условии не превышения стандартным отклонением доходности уровня 2.5%, выдал ожидаемую месячную доходность 0.65% и коэффициент Шарпа 0.26.
Таблица 4: Реализованные доходности, стандартные отклонения и коэффициенты Шарпа портфелей Р1, Р2 и Р3
| P1 | Р2 | Р3 | |
| Mean Return | 0.46% | 0.52% | 0.65% |
| StDev | 1.74% | 1.72% | 2.50% |
| Sharpe Ratio | 0.26 | 0.30 | 0.26 |
С помощью инструментария PCI построим график динамики портфеля Р3, включив в состав базовой части уже пять активов с соответствующими весами, а в состав котируемой части – индекс Dow Jones Industrial Average.
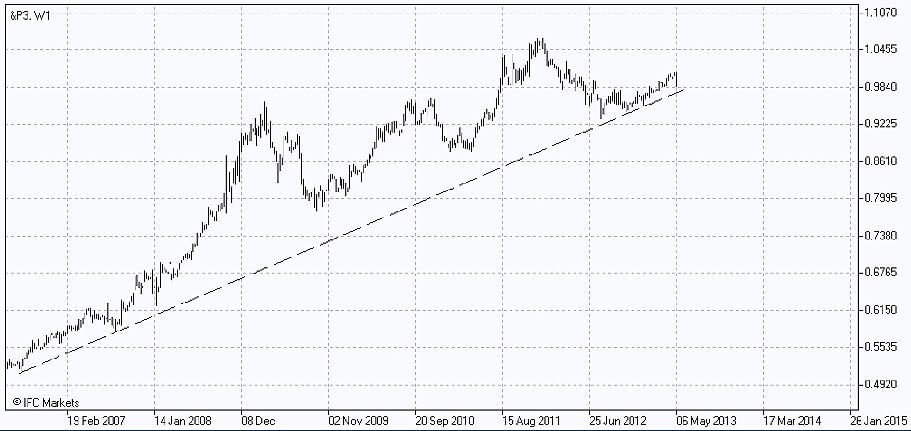
Мы по-прежнему можем наблюдать растущую структуру. Рост за весь исследуемый период оказался более значительным, чем у портфеля Р2, но и колебания во время кризисов выглядят более существенными – прямое следствие увеличения допустимого риска.
Для полноты картины построим также портфель для инвестора, стремящегося максимально избавится от рисков за счет диверсификации. Для этого прибегнем к процедуре оптимизации весов доступных активов и поиска минимального значения стандартного отклонения. Полученный портфель Р4 характеризуется следующим набором весов:
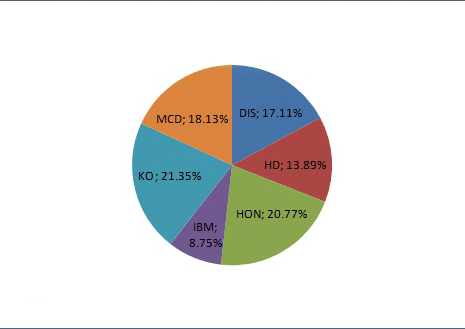
Из диаграммы следует, что на этот раз наибольший весовой коэффициент выпал на долю акций KO (21.35%), ведь именно для этого актива мы получили наименьшее стандартное отклонение из исходных данных. Затем по убыванию весов расположились HON (20.77%), MCD (18.13%), DIS (17.11%), HD (13.89%) и IBM (8.75%). Этот портфель характеризуется ожидаемой доходностью 0.45%, стандартным отклонением 1.60% и коэффициентом Шарпа 0.28.
Таблица 5: Реализованные доходности, стандартные отклонения и коэффициенты Шарпа портфелей Р1, Р2, Р3 и Р4
| P1 | Р2 | Р3 | Р3 | |
| Mean Return | 0.46% | 0.52% | 0.65% | 0.45% |
| StDev | 1.74% | 1.72% | 2.50% | 1.60% |
| Sharpe Ratio | 0.26 | 0.30 | 0.26 | 0.28 |
Инструментарий PCI вновь поможет построить график портфеля и оценить его поведение на исследуемом периоде времени по отношению к индексу Dow Jones Industrial Average.
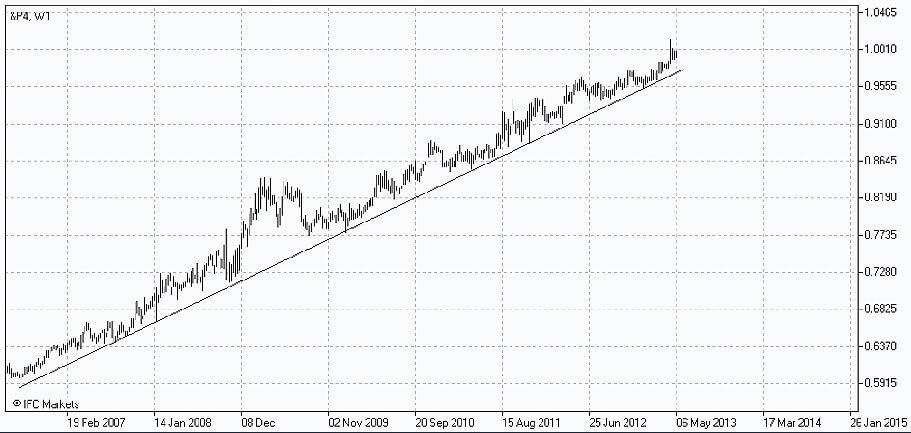
Поразительно, насколько спокойным выглядит поведение портфеля Р4. Хотя показатели абсолютного роста за весь период ниже, чем у построенных ранее портфелей, сравнительно узкий диапазон колебаний, отражающий более низкую волатильность, имеет свои преимущества.
Если изобразить все четыре портфеля (Р1, Р2, Р3, Р4) в координатах риск-доходность, мы можем утверждать лишь то, что портфель Р2 (максимальный коэффициент Шарпа) предпочтительнее «случайного» портфеля Р1, так как его расположение (выше и левее) говорит о более высокой доходности и более низком стандартном отклонении.
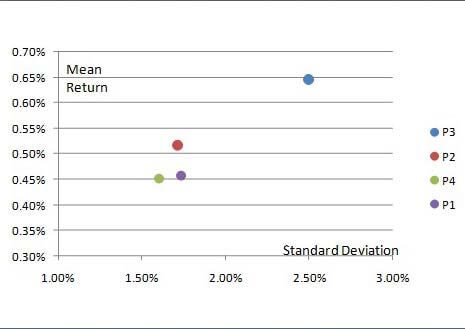
Выбор между портфелями Р2, Р3 и Р4 будет зависеть от индивидуальных предпочтений и ограничений инвестора. Если инвестор готов принять относительно высокий уровень риска, его выбор сместится в сторону портфеля Р3 с самой высокой (из рассматриваемых вариантов) ожидаемой доходностью. Если инвестор стремится к минимизации рисков, его выбором может стать портфель Р4, обладающий самым низким стандартным отклонением (из рассматриваемых вариантов). Портфель Р2 мы бы назвали сбалансированным портфелем, обладающим лучшей отдачей доходности на единицу риска.
Графики, построенные с помощью метода PQM и инструментария PCI, наглядно подтверждают возможности использования принципов современной портфельной теории. Основываясь на количественных оценках риска, доходности и ковариации различных активов мы нашли множество «удачных» портфелей, которые систематически обыгрывали рынок на протяжении последних лет и при этом отвечали самым разным инвестиционным предпочтениям. Наш анализ строился всего лишь на семи активах (6 акций + индекс) из одного класса финансовых инструментов. Потенциальный выигрыш от диверсификации может быть существенно увеличен, если добавить в анализ прочие классы активов, которые бы имели более низкую или отрицательную корреляцию друг с другом. Сложно даже представить, какие в этом случае могут появиться возможности использования метода PQM для анализа рынков и торговли.
Начало статьи читайте в разделе "Оптимизация портфеля с помощью метода PQM (часть 1)"
Предыдущие статьи
- Четвертый постулат Доу: на службе инвестора
- Портфельный спред на основе непрерывных фьючерсов
- Портфель Шарпа | “Тройка лидеров” - DJIA, S&P500, Nasdaq 100
- Поиск «хорошего» и «плохого» портфеля с помощью метода Портфельного Котирования PQM
- Оптимизация портфеля с помощью метода PQM (часть 1)
- Портфель Акций | Составление Портфеля с помощью Метода Портфельного Котирования PQM
