- Торговля
- Программная Торговля
- Торговые Советники NetTradeX
- Создание нейронной сети на языке NTL+
Создание нейронной сети на языке NTL+
Введение
Искусственные нейронные сети - математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей - сетей нервных клеток (нейронов) мозга.
В текущий момент нейронные сети достаточно широко применяются во многих задачах распознавания, классификации, ассоциативной памяти, определения закономерностей, прогнозирования и т.д.
Для работы с нейронными сетями существуют отдельные математические продукты или дополнительные модули к основным математическим пакетам, предоставляющие широкие возможности по конструированию сетей различных типов и конфигураций.
Мы же попробуем создать свою собственную сеть с нуля при помощи языка NTL+, а заодно попробуем его возможности объектно-ориентированного программирования.
Выбор задачи
В этой статье давайте проверим гипотезу, что по прошедшим барам можно предсказать с определенной вероятностью вид будущего бара: снижающийся или растущий.
Данная задача относится к задачам классификации. В нашем распоряжении также доступна обширная историческая информация по финансовым инструментам, что позволит использовать эти исторические данные для получения "экспертной" оценки. В связи с этим, будем создавать сеть на основе многослойного персептрона.
Итак, попытаемся создать сеть, предсказывающую по ценам закрытия k баров, вид последующего бара. Если его цена закрытия выше цены закрытия предыдущего бара, то примем желаемое значение выхода за 1 (цена выросла). В остальных случаях, примем желаемое значение выхода за 0 (цена не изменилась или упала).
Конструирование сети
В общем виде многослойный персептрон имеет один входной слой, один или несколько скрытых слоев и один выходной слой. Единственного скрытого слоя достаточно для преобразования входов таким образом, чтобы линейно разделить выходное представление. Использование большего числа скрытых слоев часто приводит лишь к заметному снижению скорости обучения сети без заметного выигрыша в качестве обучения.
Остановимся на сети с одним входным слоем, одним скрытым и одним выходным слоем. На следующем рисунке представлена архитектура нашей сети в общем виде. x1 - xn - входы (цены закрытия), wi,j - веса ребер, выходящих из узла i и входящих в j;
y1 - ym нейроны скрытого слоя, o1 - ok выходы сети.
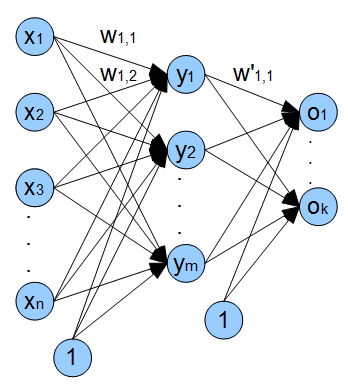
Также в сети используются входы смещения (bias inputs). Использование этих входов обеспечивает возможность нашей сети по сдвигу активационной функции вдоль оси абсцисс, тем самым сеть может не только изменять крутизну активационных функций, но и обеспечивать ее линейное смещение.
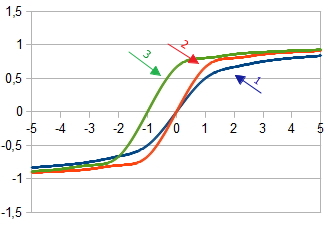
1. График активационной функции 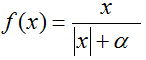 при
при 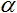 = 1
= 1
2. График активационной функции 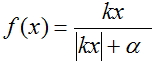 при
при 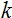 =2 и
=2 и 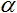 = 1
= 1
3. График активационной функции при задании смещения 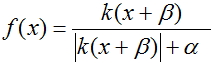 при
при 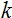 =2,
=2, 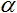 = 1 и
= 1 и 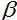 = 1
= 1
Значения для каждого узла сети будем вычислять по формуле:
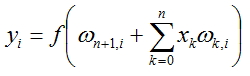 , где f(x) - функция активации, а n-число узлов в предыдущем слое.
, где f(x) - функция активации, а n-число узлов в предыдущем слое.
Функции активации
Функция активации вычисляет выходной сигнал, получаемый после прохождения сумматора. Искусственный нейрон обычно представляют, как некоторую нелинейную функцию от единственного аргумента. Наиболее часто используются следующие функции активации:
Функция Ферми (экспоненциальная сигмоида):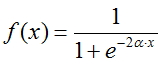
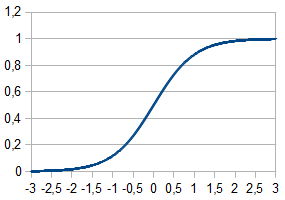
Рациональная сигмоида:
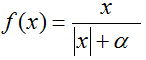
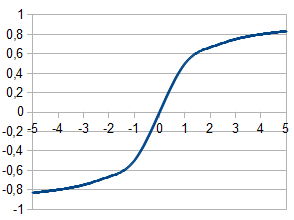
Гиперболический тангенс:
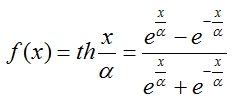
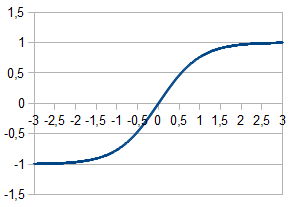
Для определения выходов каждого слоя была выбрана рациональная сигмоида, так как ее вычисление занимаем меньше всего процессорного времени.
Процесс обучения сети
Для обучения нашей сети реализуем метод обратного распространения ошибки. Этот метод является итеративным алгоритмом, используемый с целью минимизации ошибки работы многослойного персептрона. Основная идея алгоритма: после вычисления выходов сети, вычисляются поправки 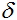 каждого узла и ошибкa w для каждого ребра, при этом вычисление ошибки происходит в направлении от выходов сети к ее входам. Затем происходим корректировка весов w в соответствии с вычисленным значением ошибки. Этот алгоритм накладывает единственное требование на активационную функцию - она должна быть дифференцируемой. Сигмоиды и гиперболический тангенс удовлетворяют этому требованию.
каждого узла и ошибкa w для каждого ребра, при этом вычисление ошибки происходит в направлении от выходов сети к ее входам. Затем происходим корректировка весов w в соответствии с вычисленным значением ошибки. Этот алгоритм накладывает единственное требование на активационную функцию - она должна быть дифференцируемой. Сигмоиды и гиперболический тангенс удовлетворяют этому требованию.
Итак, для процесса обучения нам понадобится выполнить следующую последовательность действий:
- Инициализировать веса всех ребер малыми случайными значениями
- Для всех выходов сети подсчитать поправку
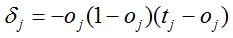 , где oj - вычисленный выход сети, tj - фактическое значение
, где oj - вычисленный выход сети, tj - фактическое значение - Для каждого узла, кроме последнего вычислить поправку по формуле
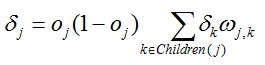 , где wj,k
веса на ребрах, выходящих из узла, для которого вычисляется поправка, а
, где wj,k
веса на ребрах, выходящих из узла, для которого вычисляется поправка, а 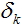 вычисленные поправки для узлов, находящихся ближе к выходному слою.
вычисленные поправки для узлов, находящихся ближе к выходному слою.
- Для каждого ребра сети вычислить поправку:
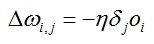 , где oi рассчитанный выход узла из которого выходит ребро, для которого вычисляется ошибка, а
, где oi рассчитанный выход узла из которого выходит ребро, для которого вычисляется ошибка, а 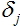 вычисленная поправка узла в который входит указанное ребро.
вычисленная поправка узла в который входит указанное ребро. - Откорректировать значения весов для всех ребер:
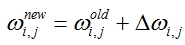
- Повторять шаги 2 - 5 для всех обучающих примеров или пока не будет достигнут выбранный критерий качества обучения.
Подготовка входных данных
Для осуществления процесса обучения сети необходимо подготовить входные данные, качественные входные значения оказывают значительное влияние на работу сети и скорость стабилизации ее коэффициентов w, то есть, фактически, на сам процесс обучения.
Все входные вектора рекомендуется нормализовать, чтобы их компоненты лежали в диапазоне [0;1] или [-1;1]. Нормализация делает все входные вектора равноправными в процессе обучения сети, тем самым обеспечивается корректная процедура её обучения.
Будем нормализовывать наши входные вектора - преобразовывать значения их компонент к диапазону [0;1], для этого воспользуемся следующий формулой:
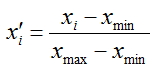
В качестве компонент вектора будут выступать цены закрытия баров, при этом в качестве входов будут подаваться цены закрытия баров c индексами [n+k;n+1], где k размерность входного вектора. Желаемое значение будем определять на основе n бара. Его величину будем устанавливать, руководствуясь следующей логикой: если цена закрытия для n бара больше цены закрытия для n+1 бара (цена возросла) принимаем желаемое значение равным 1, в случае уменьшения или равенства цены выставляем его равным 0;
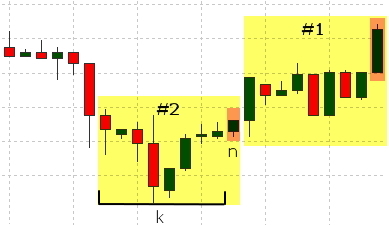
На рисунке выделены желтым цветом бары, участвующие для формирования каждого набора данных (#1, #2), оранжевым выделен бар, используемый для определения желаемого значения.
На процесс обучения сети также влияет порядок предоставления данных в процессе обучения. Процесс обучения
проходит более стабильно, если входные вектора соответствующие 1 и 0 подавать равномерно.
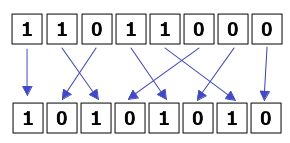
Также сформируем отдельную группу данных, используемую для оценки эффективности работы нашей сети. На этих данных сеть обучаться не будет, и они будут использоваться только для вычисления ошибки по методу наименьших квадратов. В тестовую группу данных добавим 10% исходных примеров. В результате, 90% примеров будем использовать для обучения и 10% для оценки.
Функция, вычисляющая ошибку по методу наименьших квадратов, выглядит следующим образом:
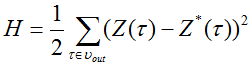 ,
,
где 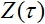 - выходной сигнал сети и
- выходной сигнал сети и 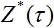 - требуемое значение выходного сигнала.
- требуемое значение выходного сигнала.
Теперь рассмотрим код скрипта, подготавливающего входные вектора для нашей нейронной сети.
Рассмотрим класс DataSet - набор данных. Класс в себя включает:
- Массив векторов входных значений - input
- Формируемое выходное значение - output
- Метод Normalize - нормализация данных
- Метод OutputDefine - определение фактического значения по соотношению цен
- Метод AddData - запись значений в массив входного вектора и переменной с фактическим значением
- Метод To_file - сбор данных в единый массив для последующей записи в файл
Теперь рассмотрим код программы, используемый в функции Run() и выполняющий следующую последовательность действий:
- Загрузка всей истории, имеющейся в терминале во внутренний массив. Загрузка осуществляется по тому символу и таймфрейму для которого на данный момент выводится график.
- Обрезание массива баров до размера, кратному длине входного вектора + выходное значение
- Формирования массива входных векторов. Нормализация этих векторов. Определение желаемого значения 0 или 1
- Формирование массива отсортированных входных векторов, где вектора соответствующие 0 и 1 последовательно чередуются
- Запись основной части массива с отсортированными входными векторами в файл с данными и запись оставшейся части данных в массив для тестирования и, в последствии, оценивания по методу наименьших квадратов)
В этом файле вам также понадобится объявить глобальную переменную int state = 0, которая необходима для осуществления чередования входных векторов.
Создание классов сети
Для нашей сети понадобятся:
- Экземпляр класса layer для связывания входного и скрытого слоя сети
- Экземпляр класса layer для связывания скрытого и выходного слоя сети
- Экземпляр класса net для соединения слоев в нашей сети
Создаем класс layer - слой
Итак, нам понадобится класс, содержащий следующие свойства и методы:
- Массив для хранения входов сети 'input'
- Массив для хранения выходов сети 'output'
- Массив для хранения поправок 'delta'
- Двумерный массив для весов ребер 'weights'
- Метод 'LoadInputs' для присвоения входам слоя значений, заданных во входном массиве
- Метод 'LoadWeights' для загрузки значений весов слоя, сохраненных на жестком диске
- Метод 'SaveWeights' для сохранения значений весов слоя на жесткий диск
- Конструктор, выделяющий нужный объем памяти для используемых массивов
- Метод 'RandomizeWeights', заполняющий веса случайными значениями
- Метод 'OutputCalculation', вычисляющий значения выходов
- Методы 'CalculatingDeltaLast' и CalculatingDeltaPrevious, вычисляющие значения поправок
- Метод 'WeightsCorrection', корректирующий значения весов
- Вспомогательные (диагностические) методы для вывода информации на экран:
- PrintInputs() - печать входов слоя
- PrintOutputs() - печать выходов слоя (вызывается после вычисления выхода при помощи 'OutputCalculation')
- PrintDelta() - печать поправок для слоя (вызывать после вычисления поправок при помощи 'CalculatingDeltaLast' или 'CalculatingDeltaPrevious')
- PrintWeights() - печать весов w для слоя
- Метод 'Calculate', связывающий наши слои для вычисления выхода сети. Впоследствии этот метод будет использоваться для работы с обученной сетью.
- Метод 'CalculateAndLearn', вычисляющий выходы, поправки и ошибки. Для вычисления выходов мы вызовем предыдущий метод, а для поправок и ошибок он будет вызывать соответствующие методы каждого слоя
- Метод 'SaveNetwork', сохраняющий коэффициентов сети.
- Метод 'LoadNetwork', загружающий коэффициентов сети.
- Создает объект NT класса net
- Считывает коэффициенты w и загружаем их в NT
- Создает массивы входов и выходов сети
- В цикле считывает входы и помещает их в массив 'x', считывает выходы и помещаем их в массив 'reals'
- Вычисляет выход сети, подавая на вход массив 'x'
- Вычисляет ошибку error, как сумму квадратов разностей между всеми вычисленными значениями и фактическими значениями
- При подходе к концу файла выводим значение ошибки и завершаем работу скрипта
Получившийся класс вынесем в отдельный файл. Кроме того, в этом же файле будет храниться конфигурация сети: количество узлов во входном, скрытом и выходном слоях. Эти переменные вынесены вне класса для того, чтобы их значения также использовались в скрипте для подготовки входных данных.
Также нам понадобятся вспомогательные функции, которые мы поместим вне классов. Это будут 2 функции: нормализация входного вектора и функция активации.
Создаем класс net - сеть
Нам понадобится класс, объединяющий наши слои в единую сеть, поэтому такой класс должен содержать:
Проверка работы сети
В этом подразделе проверим работу нашей сети на элементарном примере, с его помощью определим, правильность классификации входных векторов. Для этого будем использовать сеть с двумя входами, двумя узлами скрытого слоя и одним выходом. Параметр nu установим равным 1. Входные данные будут представлять собой чередующиеся наборы следующего содержания:
вход 1,2 и желаемое значение 1
вход 2,1 и желаемое значение 0
В файле они будут заданы в таком виде:
Подавая на вход разное количество обучающих примеров можно увидеть, как происходит процесс обучения нашей сети.
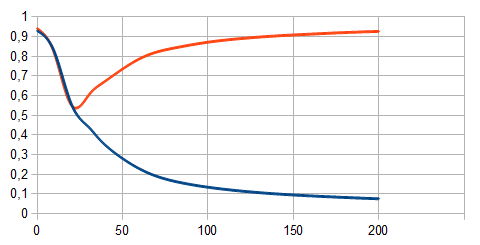
Красная линия на графике соответствует обучающему примеру, соответствующему 1. Синяя линия - соответствующему 0. По оси абсцисс откладывается номер обучающего примера, по оси ординат вычисленное значение сети для обучающего примера. Видно, что при малом количестве примеров (25 и менее) сеть не распознает различные входные вектора, при большем количестве - происходит явное разделение на 2 класса.
Оценка работы сети
Для оценки эффективности обучения воспользуемся функцией вычисляющей ошибку по методу наименьших квадратов. Для этого создадим утилиту со следующим кодом и запустим ее. Для ее работы понадобятся два файла: "test.txt" - данные и желаемые значения, используемые при вычислении ошибки и "NT.txt" - файл с уже вычисленными коэффициентами для работы сети.
Данный скрипт выполняет следующую последовательность действий:
Создаем индикатор
Создадим индикатор, показывающий решение сети о следующем баре при помощи гистограммы. Логика работы индикатора простая. Значение 0 будет соответствовать снижению значения следующего бара, значение 1 - увеличение значения, а 0.5 - равновероятные события уменьшения и увеличения цены закрытия. Для вывода в отдельном окне укажем
#set_indicator_separate, также нужно указать файл, в котором определен класс net, его мы подключаем в строке
#include "Libraries\NN.ntl". Кроме этого нам понадобится переменная для хранения рассчитанного выхода сети для заданного входа, если выходное значение одно, то достаточно единственной переменной, но сеть может иметь несколько выходов, так что в общем виде нам потребуется массив значений: его мы объявляем в строке array . В функции инициализации мы определяем параметры нашего индикатора, его тип, связываем значения гистограммы с двумя буферами значений. Также нам понадобится восстановить параметры нашей сети, то есть загрузить в нее все весовые коэффициенты, вычисленные в процессе обучения. Это осуществляется при помощи метода LoadNetwork(string s) объекта NT, с единственным параметром - именем файла, содержащем весовые коэффициенты. В функции Draw мы формируем входной вектор x соответствующий ценам закрытия баров с индексами [pos+inputVectorSize-1; pos],
где pos - номер бара для которого вычисляется значение, а inputVectorSize длина входного вектора. В конце вызывается метод Calculate объекта NT, возвращающий массив значений (если в нашей сети несколько выходов), но так как у нас выход только один - используем элемент массива с индексом 0.
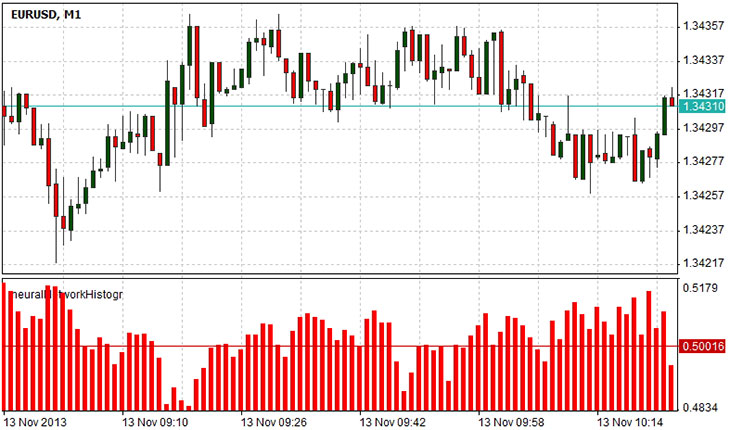
Показанная гистограмма отображает прогноз сети для следующего бара. Значения от 0.5 до 1 говорят о том, что вероятность последующего возрастающего бара больше вероятности снижающегося бара. Значения от 0 до 0.5 - вероятность снижающегося бара больше вероятности растущего. Значение 0.5 соответствует состоянию неопределенности: следующий бар может как возрастать, так и снижаться.
Резюме
Нейронные сети являются мощным инструментом по анализу данных. В статье был показан процесс создания нейронной сети с использованием объектно-ориентированного программирования в языке NTL+. Использование объектно-ориентированного подхода позволило упростить код и сделать его гораздо более удобным для многократного использования в будущих скриптах. В приведенной реализации нам понадобилось создать класс layer описывающий слой нейронной сети и класс net для описания сети в целом. Класс net мы использовали для индикатора, определения величины ошибки и вычисления собственных весов сети. Кроме того, было показано, как можно использовать обученную сеть на примере индикатора-гистограммы, показывающем прогноз сети по изменению цены.
