- Trading
- Trading Automático
- Asesores para NetTradeX
- Creación de una red neuronal en NTL +
Creación de una red neuronal en NTL +
Introducción
Redes neuronales artificiales – modelos matemáticos o sus implementaciones software o hardware mathematical models and their software or hardware que están construidas en el principio de la organización y funcionamiento de las redes neuronales biológicas - redes de células neuronales (neuronas) del cerebro.
Actualmente, las redes neuronales se usan ampliamente en muchas tareas de reconocimiento, clasificación, memoria asociativa, patrones de determinación, previsiones etc.
Con el fin de trabajar con redes neuronales, existen productos matemáticos independientes y módulos adicionales para mayores paquetes matemáticos de software, que proporcionan amplias oportunidades de construcción de redes de diferentes tipos y configuraciones.
Nosotros, por otra parte, intentaremos crear nuestra propia red neuronal desde el cero por los medios del lenguaje NTL+ y probar al mismo tiempo sus capacidades de programación orientadas a objetos.
Elección de una tarea
En este artículo verifiquemos la hipótesis de que por motivos de barras anteriores es posible predecir con cierta probabilidad el tipo de la siguiente barra: ascendente o descendente.
Esta tarea esta relacionada con las de clasificación. Tenemos también información histórica extensiva sobre los instrumentos financieros en nuestra diposición, que permite usar los datos históricos para obtener el resultado deseado (experto).
Ahora, vamos a crear una red que en la base de los precios de cierre de las barras k predice el tipo de la barra siguiente. Si el precio de cierre es más alto que el precio del cierre de la barra anterior, supongamos que el resultado deseado es de 1 (el precio creció). En otros casos, supongamos que el resultado deseado es de 0 (el precio no creció o cayó).
Construcción de la red
En general, un perceptrón multicapa tiene una capa de entrada, una o varias capas ocultas y una capa de salida. Tener una sola capa oculta es suficiente para la transformación de las entradas, de tal manera para dividir linealmente la representación de entrada. El uso de más capas ocultas a menudo causa disminución significativa en la velocidad de la formación de una red sin ninguna ventaja notable en la calidad del aprendizaje.
Vamos a instalarse en una red con una capa de entrada, una oculta y una capa de salida. La siguiente figura muestra la arquitectura de nuestra red en términos generales.
x1 - xn - entradas (precios de cierre), wi,j - pesos de los bordes que viene de nodo i y va al nodo j;
y1 - ym neuronas de la capa oculta, o1 - ok salidas de la red.
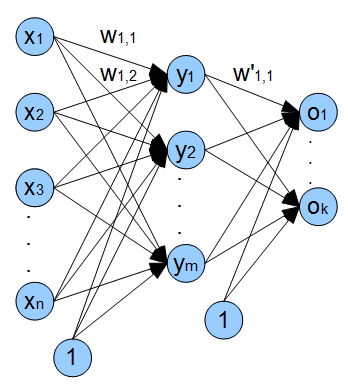
Además hay entradas de sesgos (bias inputs) en la red. El uso de estas entradas proporciona la capacidad de nuetsra red para cambiar la función de activación a lo largo del eje x, por lo tanto, la red no solo puede cambiar la inclinación del función de activación, sino también proporcionar su desplazamiento lineal.
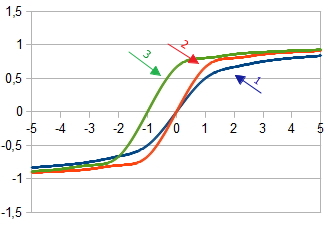
1. Gráfico de la función de activación 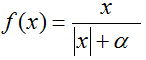 at
at 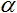 = 1
= 1
2. Gráfico de la función de activación 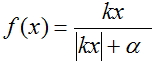 en
en 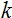 =2 y
=2 y 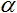 = 1
= 1
3. Gráfico de la función de activación con el desplazamiento 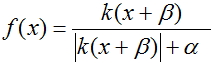 en
en 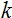 =2,
=2, 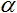 = 1 y
= 1 y 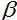 = 1
= 1
El valor de cada nodo se calculará según la fórmula:
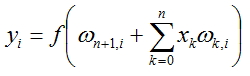 , where f(x) - funcción de activación, y n número de nodos en la capa anterior.
, where f(x) - funcción de activación, y n número de nodos en la capa anterior.
Funciones de Activación
La funciones de activación calculan la señal de salida, recibida dspués de pasar el acumulador. La neurona artificial en general está representada como un función no lineal del único argumento. Más se usan las siguientes funciones de activación.
Función de Fermi (sigmoide exponencial):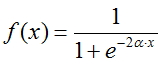
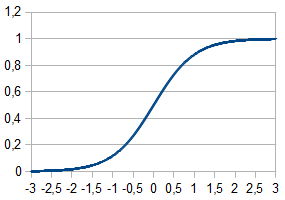
Sigmoide racional:
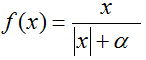
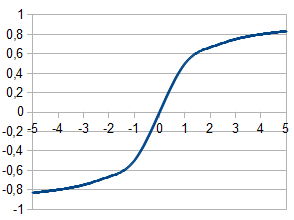
Tangente hiperbólica:
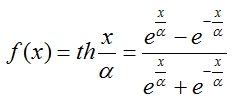
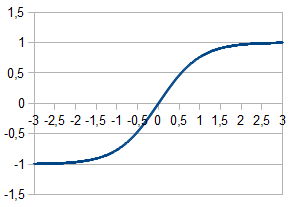
Con el fin de calcular las salidas de cada capa, fue elegido el sigmoide racional debido a que su cálculo toma menos tiempo de procesador.
Proceso de capacitación de la red
Para capacitar a nuestra red, vamos a poner en práctica el método de propagación hacia atrás. Este método es un algoritmo iterative que se usa para minimizar el error de la obra de un perceptrón multicapa. La idea fundamental del algoritmo: después de calcular las salidas de la red, se calculan los ajustes para cada nodo 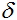 y errores ω para cada borde, mientras tanto el error de la calculación va en una dirección de las salidas de la red hacia sus entradas. Después de hace la corrección de los pesos ωen conformidad con los valores de los errores calculados. Este algoritmo impone el único requisito de que la función de activación - debe ser diferenciada. El sigmoide y la tangente hiperbólica cumplen con este requisito.
y errores ω para cada borde, mientras tanto el error de la calculación va en una dirección de las salidas de la red hacia sus entradas. Después de hace la corrección de los pesos ωen conformidad con los valores de los errores calculados. Este algoritmo impone el único requisito de que la función de activación - debe ser diferenciada. El sigmoide y la tangente hiperbólica cumplen con este requisito.
Ahora, para llevar a cabo el proceso de capacitación, necesitamos la siguiente secuencia de pasos:
- Inicializar los pesos de todos los bordes con pequeños valores aleatorios
- Calcular ajustes para todas las salidas de la red
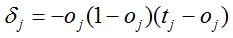 , donde oj es la salida calculada de la red, tj es el valor fáctual
, donde oj es la salida calculada de la red, tj es el valor fáctual - Para cada nodo, excepto para la última calcular un ajuste de acuerdo con la fórmula
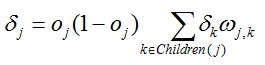 , donde ωj,k
son los pesos en los bordes, que salen del nodo, para que se calcula un ajuste y
, donde ωj,k
son los pesos en los bordes, que salen del nodo, para que se calcula un ajuste y 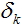 es el ajuste calculado para los nodos, siuados cerca de la capa de salida.
es el ajuste calculado para los nodos, siuados cerca de la capa de salida.
- Calcular ajustes para cada borde de la red:
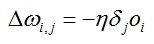 , donde oies la salida del nodo, de donde viene el borde. El error se calcula para el borde y
, donde oies la salida del nodo, de donde viene el borde. El error se calcula para el borde y 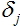 es el ajuste calculado para el nodo hacia cual va el borde especificado.
es el ajuste calculado para el nodo hacia cual va el borde especificado. - Valores de pesos correctos para todos los bordes:
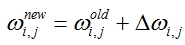
- Repita los pasos 2 - 5 para todos los ejemplos de entrenamiento o hasta que se cumpla el criterio establecido de la calidad del aprendizaje.
Preparación de los datos de entrada
Es necesario preparar los datos de entrada para realizar el proceso de entretenamiento de la red, los datos de entrada de alta calidad tienen un impacto significativo en el trabajo de la red y en la velocidad de la estabilización de sus coeficientes ω, es decir, en el proceso mismo de capacitación.
Se recomienda normalizar todos los vectores de entrada, de modo que sus componentes se encuentren en el rango [0;1] o [-1;1]. La normalización hace que todos los vectores de entrada estén en consonancia en el proceso de formación de la red, y por lo tanto se logra un proceso correcto de entrenamiento.
Vamos a normalizar nuestras vectores de entrada - transformar los valores de sus componentes a la gama [0;1], para ello vamos a aplicar la fórmula:
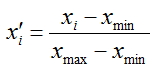
Los precios de cierre de barras se utilizan como componentes del vector. Los con los índices [n+k;n+1] se utilizarán como salidas, donde k será la dimensión del vector de entrada. Vamos a determinar el valor deseado basado en la barra n.
Vamos a formar el valor de los terrenos de la siguiente lógica: si el precio de cierre de la barra n es más alto que el precio de cierre de la barra n+1 bar (the price rose), pondremos el valor deseado de salida a 1, en el caso si el precio cae o no cambia, pondremos el valor a 0;
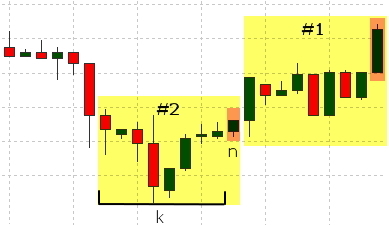
Las barras que participan en la formación de cada conjunto se resaltan en amarillo en la figura, la barra que se utiliza para determinar el valor deseado se pondrá en naranja.
La secuencia de los datos facilitados también afecta al proceso de formación. El proceso de aprendizaje se lleva más estable si los vectores de entradas correspondiente a 1 y 0 se apliquen de manera uniforme.
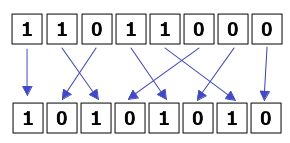
También se formará un grupo separado de los datos utilizados para evaluar el rendimiento de nuestra red. En estos datos la red no será entrenada y sólo se utilizarán para el cálculo del error por el método de los mínimos cuadrados. En el grupo de prueba de datos se añaden 10% de la muestra original. Como resultado, el 90% de los ejemplos se utiliza para la formación y el 10% para la evaluación.
La función, que calcula el error con el método de mínimos cuadrados, se ve así:
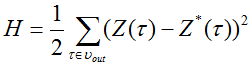 ,
,
donde 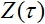 - señal de salida de la red y
- señal de salida de la red y 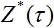 - valor deseado de la señal de salida.
- valor deseado de la señal de salida.
Ahora examinemos el código script, preparando los vectores de entrada para nuestra red neuronal.
Examinemos la clase DataSet class – conjunto de datos. La clase incluye:
- Matriz de vectores de valores de entrada - input
- Valor de salida formado - output
- Método 'Normalize' - normalización de datos
- Métod 'OutputDefine' -determinación del valor actual en relación con lo precios
- Método 'AddData' - registro de valores de la matriz de vectores de entrada y variables de valor real
- Método 'To_file' recogida de datos de la matriz común para la posterior grabación en el archivo
Examinemos ahora el código del programa, que se utiliza en la función Run() y realizando la siguiente secuencia de acciones:
- Carga de todos los datos históricos que se encuentra disponible en el terminal a una disposición interna. La carga se realiza para el símbolo y el plazo para cuales se mostrará el gráfico actual.
- Recorte de la matriz de barras al tamaño que es n veces el vector de entrada + valor de salida
- Formación de las matrices de vectores de entrada; la normalización de estos vectores; determinación del valor deseado 0 o 1
- Formación de la matriz de vectores de entrada ordenados, donde los vectores correspondientes a 0 y 1 alternan sucesivamente
- Registro de la parte principal de la matriz con los vectores de entrada ordenados en el archivo con los datos y el registro de la parte restante de los datos de la matriz para el ensayo y, posteriormente, la estimación con el método de los mínimos cuadrados.
También es necesario declarar la variable global int state = 0 en este archivo, se requiere la variable para la alternancia de vectores de entrada.
Creación de clases de la red
Para nuestra red necesitaremos:
- una instancia de la clase 'layer' para conectar las capas de entrada y ocultas de la red
- una instancia de la clase 'layer' para conectar las capas ocultas y de salida de la red
- una instancia de la clase 'net' para conectar las capas de nuestra red
Creación de la clase 'layer' - capa
Ahora vamos a necesitar la clase que contiene las siguientes propiedades y métodos:
- matriz 'input' para almacenar las entradas de la red
- matriz 'output' para almacenar las salidas de la red
- matriz 'delta' para almacenar los ajustes
- matriz bidimensional 'weights' para los pesos de bordes
- método'LoadInputs' para la asignación de los valores especificados en la matriz de entrada a las entradas de la capa
- método 'LoadWeights' para cargar los valores de pesos de la capa del disco duro
- método 'SaveWeights' para guarder los valores de pesos de la capa en el disco duro
- constructor que asigna el volumen de memoria necesario para las matrices utilizadas
- método 'RandomizeWeights' para llenar pesos con valores aleatorios
- método 'OutputCalculation' para calcular los valores de salida
- método 'CalculatingDeltaLast' y 'CalculatingDeltaPrevious' para calcular los valores de ajustes
- método 'WeightsCorrection' para corregir los valores de pesos
- métodos adicionales (diagnóstico) para mostrar información en la pantalla:
- PrintInputs() – impresión de las entradas de una capa
- PrintOutputs() - impresión de las salidas de una capa (se llama después de calcular las salidas por medios de 'OutputCalculation')
- PrintDelta() – impression de ajustes de una capa (debe llamarse después de calcular los ajustes por medios de 'CalculatingDeltaLast' o 'CalculatingDeltaPrevious')
- PrintWeights() – impression de pesos ω de la capa
- Método 'Calculate' – que vincula nuestras capas para el cálculo de la salida de la red.. Este método será usado más tarde para el trabajao con la red entrenada
- Método 'CalculateAndLearn' – para computar las salidas, ajustes y errores. Vamos a llamar al método anterior para calcular las salidas, y para los ajustes y errores se llamarán los métodos correspondientes de cada capa
- Método 'SaveNetwork' – para guarder los coeficientes (pesos) de la red.
- Método 'LoadNetwork' – para cargar los coeficientes (pesos) de la red.
- crea el objeto NT de la clase 'net'
- lee los coeficientes(pesos) ω y los carga en NT
- crea matrices de entradas y salidas de la red
- lee las entradas en un bucle y localiza en la matriz ¡ 'x', lee las salidas y localiza en la matriz 'reals'
- calcula las salidas de la red,alimentando la matriz 'x' como una entrada
- computa error como la suma de los cuadrados de las diferencias entre todos los valores calculados y los valores esperados (fácticos)
- cuando se alcanza el final del archivo, se muestra el error y terminar el trabajo del script
Quitemos la clase creada en un archivo separado. Además, este archivo también contiene la configuración de red: número de nodos de entrada, capas ocultas y capas de salida. Se colocaron estas variables fuera de la clase con el fin de que puedan ser utilizadas en la secuencia de comandos para la preparación de datos de entrada.
También necesitaremos funciones adicionales que vamos a colocar fuera de las clases. Estos son 2 funciones: la normalización de un vector de entrada y la función de activación.
Creación de la clase 'net'
Vamos a necesitar una clase que combina nuestras capas en una red conjunta, por lo tanto, tal clase debe tener:
Comprobación del trabajo de la red
En este apartado, vamos a comprobar el trabajo de nuestra red en un ejemplo elemental que se utilizará para determinar la exactitud de la clasificación de los vectores de entrada.
Para ello, vamos a utilizar una red con dos entradas, dos nodos de la capa oculta y una salida. Pondremos el parametro nu a 1. Los datos de entrada se representan como conjuntos en alternancia con el siguiente contenido:
entrada 1,2 y valor esperado 1
entrada 2,1 y valor esperado 0
Se especificarán en el archivo de la siguiente forma:
Alimentando diferentes números de conjuntos de formación a la entrada, se puede observar cómo el proceso de formación de nuestra red está avanzando.
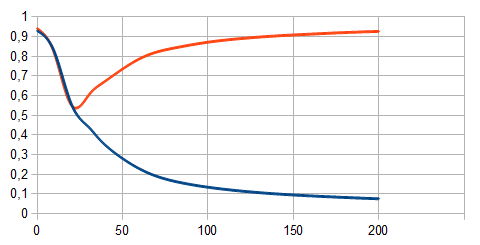
La línea roja en el gráfico muestra los conjuntos de formación correspondientes a 1. La línea azul muestra los correspondientes a 0. El número de ejemplos de entrenamiento queda cesante a lo largo del eje X y el valor calculado de la red - a lo largo del eje y. Es obvio que cuando hay pocas barras (25 o menos), la red no reconoce los diferentes vectores de entrada, cuando hay más - la división en 2 clases es evidente.
Evaluación del funcionamiento de la red
Con el fin de evaluar la eficacia de la formación, vamos a utilizar la función de calcular el error con el método de los mínimos cuadrados. Para ello, vamos a crear la utilidad con el siguiente código y ejecutarlo. Vamos a necesitar dos archivos para su: "test.txt" – datos y valores deseados (salidas) que se usan en la corrección de errores y "NT.txt" – el archivo con los coeficientes calculados (pesos) para el trabajo de la red.
El script realiza la siguiente secuencia de acciones:
Creación de un indicador
Vamos a crear un indicador que muestra la decisión de la red sobre la barra siguiente mediante un histograma. La lógica del trabajo del indicador es sencilla. El valor 0 correspondrá al valor descendente de la próxima barra, el valor 1 – al valor ascendente, y el valor 0.5 - son igualmente posibles los acontecimientos de la disminución y el aumento del precio de cierre. Para mostrar el indicador en una ventana separada, especificaremos
#set_indicator_separate, es necesario también especificar el archivo donde la clase 'net' está definida, incluiremos el archivo en la línea #include "Libraries\NN.ntl". Por otra parte, vamos a necesitar una variable para almacenar la producción calculada de la red para la entrada dada, si sólo hay un valor de salida, entonces es suficiente tener una variable, pero la red puede tener varias salidas, por lo tanto, será necesario un conjunto de los valores: lo declaramos en la línea array . En la función de inicialización de nuestro indicador especificaremos los parámetros del indicador, su tipo, los valores de vinculación de histograma con dos buffers de valores. También necesitaremos restablecer los parámetros de nuestra red, es decir, cargar en ella todos los coeficientes de peso, calculados durante el proceso de formación. Esto se hace mediante el método LoadNetwork(string s) del objeto NT, con el único parametro – nombre del archivo, que contiene los coeficientes de pesos. En la función Draw formamos un vector de entrada x correspondiente a los precios de cierre de las barras con indices [pos+inputVectorSize-1; pos], donde 'pos' – es el número de la barra para cual calculamos el valor y 'inputVectorSize' dimensión del vector de entrada. Al final, se llama el método 'Calculate' del objeto NT. Se devuelve una matriz de valores (si nuestra red tiene varias salidas), pero como tenemos una sola salida, vamos a utilizar el elemento de la matriz con el índice 0.
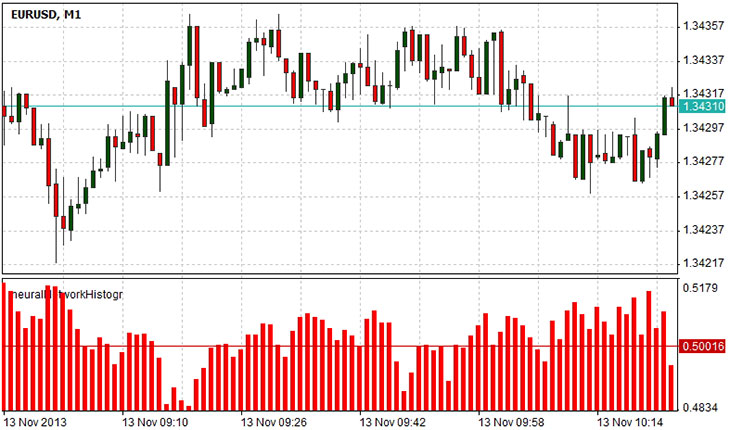
El diagrama anterior muestra el pronóstico de la red de la barra posterior. Los valores de 0,5 a 1 sugieren una posibilidad más alta que la barra posterior se subirá. Los valores de 0 a 0,5 implican mayor posibilidad de caer en lugar de aumentar. El valor 0.5 sugiere un estado de ambivalencia: la barra próxima puede ir hacia arriba o hacia abajo.
Resumen
Las redes neuronales son herramientas poderosas para el análisis de datos. Este artículo cubre el proceso de creación de una red neuronal por medio de la programación orientada a objetos en el lenguaje NTL+. El uso de la programación orientada a objetos permite simplificar el código y hacerlo mucho más reutilizable en las futuras secuencias de comandos. En la implementación presentada teníamos que crear la clase layer, definiendo una capa de la red neuronal y la clase net , definiendo la red en general. Usamos la clase 'net' para el indicador, computando el error y calculando los pesos internos de la red. En adición, se presenta cómo utilizar la red entrenada por el ejemplo del indicador de histograma, que proporciona el pronóstico de la red de la variación del precio.
