- Инновации
- Статьи о применении синтетических инструментов
- Портфельная Торговля
Оптимизация портфеля с помощью метода PQM (часть 1)
Поиск оптимальной структуры активов в портфеле, безусловно, вопрос непростой. С одной стороны, многое зависит от параметров входящих в портфель активов, с другой – от индивидуальных предпочтений и ограничений инвестора. Тем не менее, современная финансовая теория и новые методы анализа и торговли значительно упрощают этот процесс.
Одним из примеров реализации современной портфельной теории может служить метод Портфельного Котирования PQM – метод, позволяющий конструировать и анализировать многочисленные вариации портфелей, созданных из большого набора активов. Причем ценность возможностей для анализа заключается не только в наблюдении за изменением абсолютной стоимости портфеля, но и в изучении поведения портфеля по отношению к рынку или, например, альтернативному портфелю, что позволяет оперативно принимать инвестиционные решения. Результатом применения метода является создание новой финансовой единицы – синтетического инструмента (с техническим названием PCI – personal composite instrument).
В этой статье мы ограничимся набором из 6 акций американских компаний, которые, на первый взгляд, показали относительно неплохие результаты в течение последних лет. С помощью метода GeWorko мы построили портфель, показавший значительный рост в посткризисный период. В нашу выборку (с соответствующими случайными весами) вошли:
- Walt Disney Company (20%)
- Home Depot Inc. (20%)
- Honeywell International Inc. (15%)
- International Business Machines Corporation (15%)
- Coca-Cola Company (10%)
- McDonald’s Corporation (20%)
При сравнении динамики портфеля с рынком (в качестве рынка условно выступает индекс Dow Jones Industrial Average, в который входят все перечисленные акции) оказалось, что портфель систематически обыгрывал индекс до кризиса, во время него и в течение периода восстановления. Полученный за считанные секунды график PCI очень удачно иллюстрирует поведение портфеля по отношению к индексу:
График 1: Портфель против индекса Dow Jones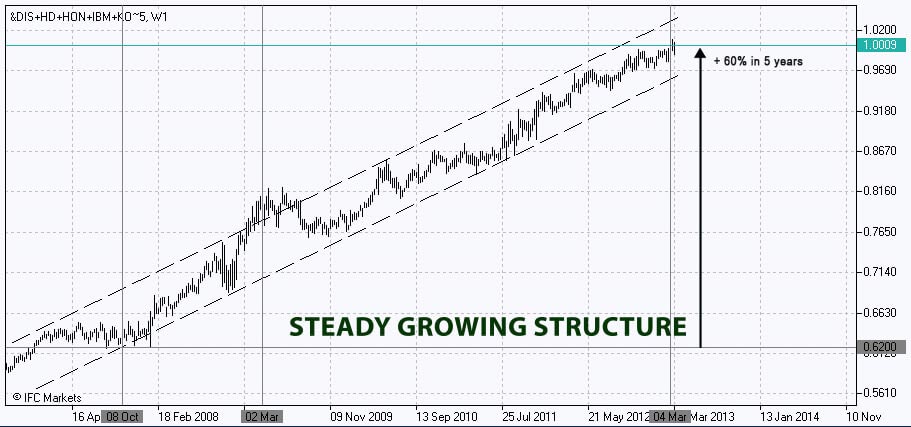
Несмотря на довольно удачную случайную подборку весов входящих в портфель активов, нам пока не известно является ли она оптимальной, то есть существуют ли другие весовые коэффициенты, обеспечивающие более низкий показатель риска на том же уровне доходности или более высокий показатель доходности при неизменном уровне риска. Если нам удастся найти такой портфель, он будет, безусловно, предпочтительнее для рационального инвестора, чем портфель со случайными весовыми коэффициентами.
Однако, определение оптимальности портфеля для инвестора, как уже говорилось выше, будет зависеть от индивидуальных предпочтений и ограничений. Без наличия конкретных требований к характеристикам портфеля мы не можем узнать, будет ли, к примеру, для инвестора портфель с более высоким уровнем дохода, но и более высоким уровнем риска, предпочтительнее первоначального портфеля. В этой связи, для целей анализа оптимальным портфелем мы будем называть портфель, который бы имел максимальную отдачу доходности на единицу риска. Этот показатель известен как коэффициент Шарпа.
В отличие от традиционной его версии, которая показывает отношение премии за риск к показателю риска, мы ограничимся отношением доходности портфеля к риску, без поправки на безрисковую ставку. Это упрощение никак не повлияет на выводы, которые позволят сравнить эффективность альтернативных инвестиционных портфелей.
Для начала вернемся к первоначальному портфелю со случайно заданными весами и определим его параметры риска и доходности. Анализ портфелей будет основываться на месячных данных по ценам закрытия шести акций по выборке январь 2005 года – апрель 2013 года. Поскольку изначальной целью было сравнение динамики портфеля с индексом (рынком), мы решили применить немного нестандартный подход и скорректировать месячные цены закрытия акций путем деления на соответствующие значения индекса. На основе логарифмов приростов доходности мы рассчитали средние месячные значения доходности и стандартные отклонения доходности для шести рядов данных. Результаты вычислений представлены в таблице ниже:
Таблица 2: Реализованные доходности, стандартные отклонения и коэффициенты Шарпа в сравнении с портфелем Р1
| DIS | HD | HON | IBM | KO | MCD | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 |
Оказалось, что наибольшую (0.77%) среднюю месячную доходность (в сравнении с индексом) показали акции MCD, наименьшую – акции HD (0.24%). Наименьшим стандартным отклонением отметились акции KO (3.95%), наибольшим – акции HD (5.73%). Кроме того, мы рассчитали упрощенную версию коэффициента Шарпа, показывающую отношение доходности актива к риску. Самый высокий коэффициент (0.19) у акций MCD, показавших наибольшую отдачу доходности на единицу риска. Этот факт позволяет нам предполагать, что именно у акций MCD будет самый высокий весовой коэффициент в «оптимальном» портфеле. Для продолжения анализа нам также понадобятся характеристики взаимосвязи шести активов между собой – коэффициенты ковариации. Ковариационная матрица рассчитана на той же выборке месячных данных.
Имея все необходимые входные параметры и предполагая, что найденные значения доходности и стандартного отклонения для шести бумаг являются лучшими оценками ожидаемых доходностей и рисков, мы можем приступить к формированию портфелей. Напомним, что исходные данные уже были скорректированы на значения индекса, поэтому портфели, которые мы получим, уже будут отражать поведение относительно рынка.
Первый портфель (Р1), который мы получим, станет отправной точкой для поиска более удачных комбинаций активов. Это портфель со случайными весовыми коэффициентами, график которого был приведен в самом начале. Зная параметры риска и доходности шести бумаг, входящих в его состав, их веса и ковариационную матрицу, мы можем рассчитать среднюю месячную доходность портфеля и его стандартное отклонение. Нетрудно заметить, что путем комбинирования активов мы добились существенного снижения риска. Стандартное отклонение портфеля P1 составляет всего 1.74%, а доходность – 0.46%:
Таблица 3: Реализованные доходности, стандартные отклонения и коэффициенты Шарпа в сравнении с портфелем Р1 и P2
| DIS | HD | HON | IBM | KO | MCD | P1 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 |
Кроме того, по сравнению с любой из шести бумаг, портфель обладает гораздо более высокой отдачей доходности на единицу риска, о чем свидетельствует коэффициент Шарпа (0.26), который в итоге и будет определять эффективность портфеля.
Теперь, зная характеристики случайного портфеля, мы можем приступить к поиску такой комбинации активов, которая бы наилучшим образом соответствовала нашим предпочтениям и ограничением. Как уже говорилось, основным показателем оптимальности портфеля мы выбрали коэффициент Шарпа. Изменяя веса шести бумаг, входящих в портфель, нам нужно найти такую комбинацию, которая соответствовала бы максимально возможному отношению доходности к риску. Единственные ограничения на поиск решения, которые мы задаем, заключаются в том, что весовые коэффициенты должны быть не меньше нуля, а их сумма должна быть равна 100%, чтобы сохранить возможность сравнения портфелей.
Решение приводит нас к следующему составу портфеля: как мы и ожидали, самый большой вес (32.67%) получили акции MCD, поскольку именно они имели самый высокий коэффициент Шарпа. Затем по убыванию весов расположились DIS (19.33%), HON (19.04%), HD (10.96%), KO (10.28%) и IBM (7.71%):
Диаграмма структуры портфеля Р2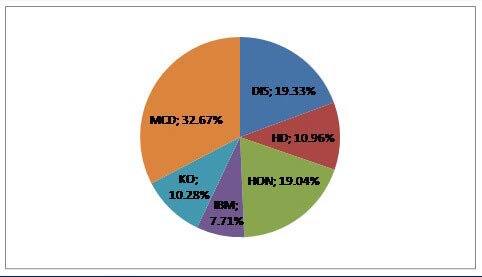
В результате, полученный путем изменения весов для максимизации коэффициента Шарпа, портфель (Р2) показал однозначно лучшие показатели, чем портфель со случайными весовыми коэффициентами (Р1):
| DIS | HD | HON | IBM | KO | MCD | P1 | P2 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% | 0.52% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% | 1.72% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 | 0.30 |
Максимизированный коэффициент Шарпа для портфеля Р2 составил 0.3. Это значение выше, чем у портфеля Р1 (0.26), не говоря уже об индивидуальных параметрах активов. Причем строго лучше оказался как показатель доходности (0.52%), так и стандартного отклонения (1.72%). Вывод – полученный максимизацией коэффициента Шарпа портфель всегда предпочтительнее для рационального инвестора (помним о предположении нашего анализа о том, что рассчитанные показатели риска и доходности являются их лучшими оценками).
С помощью инструментария PCI мы можем легко построить найденный нами «оптимальный» портфель, введя полученные весовые коэффициенты для шести акций, и соотнеся базовую часть PCI к аналогичному по стоимости портфелю, состоящему только из индекса Dow Jones Industrial Average (см. график).
График 2: Портфель, максимизирующий коэффициент Шарпа, по отношению к индексу Dow Jones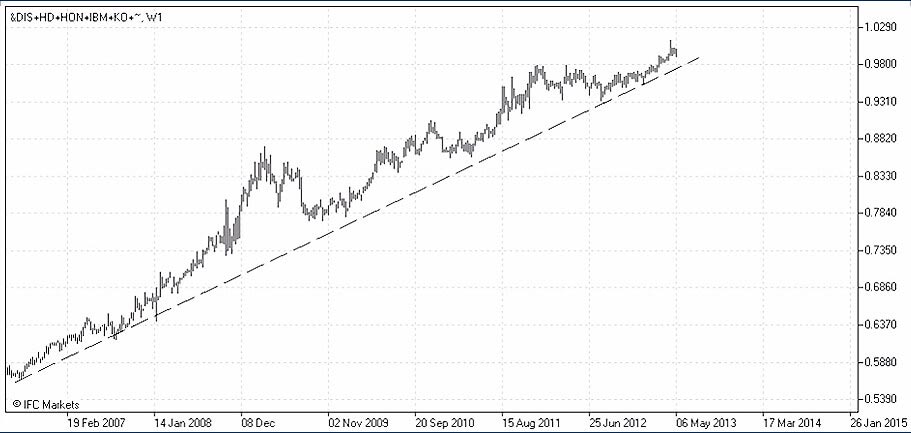
Как и в предыдущем случае со «случайным» портфелем Р1, мы получаем практически непрерывно растущую в течение последних 7 лет структуру, волатильность которой заметно возрастает во времена экономической нестабильности.
Тем не менее, подчеркнем, что это оптимальный портфель только для нас, поскольку мы избрали коэффициент Шарпа в качестве основного критерия оптимальности. Мы можем лишь утверждать, что при существующих входных параметрах нет другого портфеля, который бы позволял достичь более высокой доходности (>0.52%) при заданном уровне риска (1.72%), а также нет портфеля, который был бы менее рискованным (<1.72%) при заданной доходности (0.52%). Однако, возможна ситуация, что инвестор готов и обладает объективными возможностями пойти на увеличение риска, чтобы достичь более высокий уровень доходности, или же наоборот, инвестор стремится получить минимально рискованный портфель из доступных активов.
Продолжение статьи читайте в разделе "Оптимизация портфеля с помощью метода PQM (часть 2)"
Предыдущие статьи
- Четвертый постулат Доу: на службе инвестора
- Портфельный спред на основе непрерывных фьючерсов
- Портфель Шарпа | “Тройка лидеров” - DJIA, S&P500, Nasdaq 100
- Поиск «хорошего» и «плохого» портфеля с помощью метода Портфельного Котирования PQM
- Оптимизация портфеля с помощью метода PQM (часть 2)
- Портфель Акций | Составление Портфеля с помощью Метода Портфельного Котирования PQM
